

Here is a sample of computation times on my machine for problems of size cvxopt: CVXOPT's default (general) solver.In this benchmark, I compared four methods: Leaving it to None will callĬVXOPT's default solver for Linear Cone Programs, which should be lessĮfficient than GLPK as it solves a more general class of problems. You can choose which solver to use via the solver keyword argument, forĮxample solver='glpk' to use GLPK. lp ( c, G, h, solver = solver ) return array ( sol ). \(()\): from numpy import array, eye, hstack, ones, vstack, zeros def cvxopt_solve_minmax ( n, a, B, x_min =- 42, x_max = 42, solver = None ): c = hstack (]) # cvxopt constraint format: G * x <= h # first, a + B * x <= x G1 = zeros (( n, n + 1 )) G1 = B G1 = - ones ( n ) h1 = - a # then, x_min <= x <= x_max x_min = x_min * ones ( n ) x_max = x_max * ones ( n ) G2 = vstack (), hstack ()]) h2 = hstack () c = cvxopt. If there are people interested in such a library, I'll properly document it and polish it.Here is the function that solves the LP corresponding to an instance Today the library does what I need it for, but I would love to get some feedback about the API design, the code style, and the usability. You can add hundreds of thousands of variables, and it will always take a negligible amount of time to instantiate the problem before solving it. Println!("a + b = ", solution.eval(a + b))
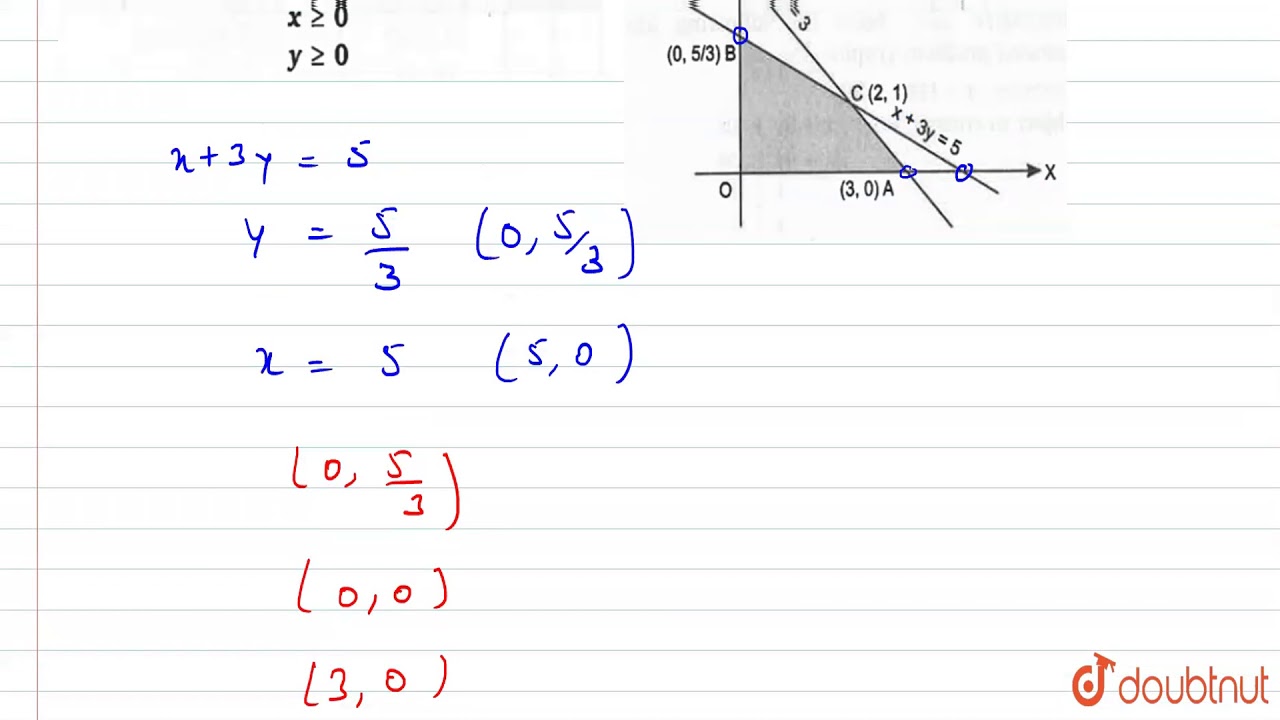
A linear problem looks like : Minimize x1 + 2*x2 + 3*x3 Linear programming is the field optimization that studies how to find the minimum value of a linear function (with multiple variables) under a set of linear constraints.
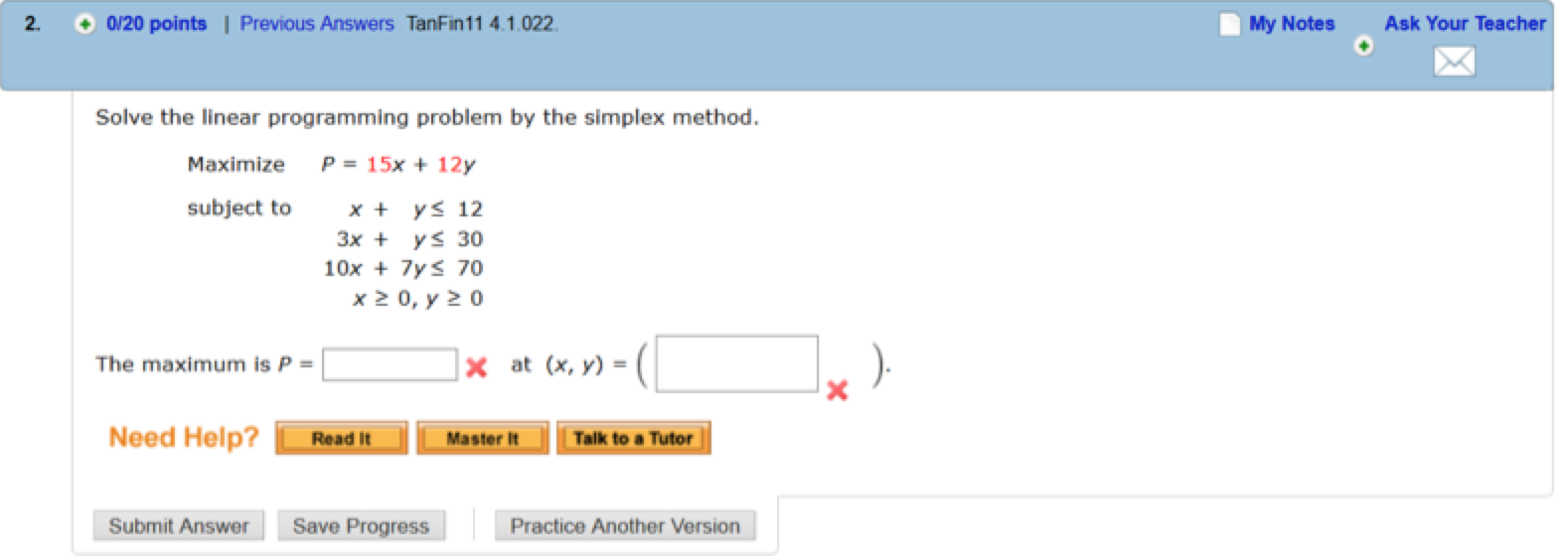
If you want, you can just jump to the code.

This post ended being longer than what I planned.


 0 kommentar(er)
0 kommentar(er)
